The Knot Series #1: Well, Why Knot? | Knots: More than Just Tangled Earphones

Knots — annoying, complicated loops that frustrate you when all you wanted was to enjoy some music on your bus ride, only to find your earphones hopelessly tangled. Or maybe it’s your crochet project all knotted up, leaving you tied in knots. While you might associate knots with shoelaces or strings, they’re more than just everyday nuisances. Knots are complex interlacements of flexible materials that form lumps, and they’ve been a part of science for quite a long time, catching the attention of scientists across a range of fields such as physics, chemistry, and even biology.

Knots: More than Just Tangled Earphones

With more than six billion knots and links that have been tabulated since the beginnings of knot theory in the 19th century, science continue to discover more knots by asking themselves the fundamental question: Can one knot be transformed into another by simply twisting or stretching it?

Knot theory is a branch of topology that explores how mathematical knots – loops that are tangled or twisted but are closed upon themselves - behave in three-dimensional space. The goal is to understand how these loops can be twisted, untwisted, or deformed without cutting or passing it through itself.

Types of Knots:

Knots can be classified into different types depending on how they are crossed and their complexity:

I'd like to think of proteins as “tamed” knots. They are long chains of amino acids that fold into themselves to form specific three-dimensional structure. The structure of the protein determines its function and misfolds which resemble unknots form complex topologies that may cause the protein to lose its function or cause more damage to the body by resulting in disease. This is where the knot series begins.

Why The Knot Series?

Knots are practically everywhere, and they’re something we encounter everyday. As a crafty person who also dives into other art forms like crocheting, cross-stitching and some occasional stitching, embroidery or friendship bracelet endeavors, knots may become trivial. However, knots are a part of us, and a part of what determines whether a protein will function or not. This series aims to talk about knots and it’s intertwined relation with biology.

Happy reading!

In addition, knot theory examines braids, which are essentially interwoven strands, and links, which are two or more loops entwined in space. These structures facilitate the investigation of object entanglement in three dimensions by mathematicians.

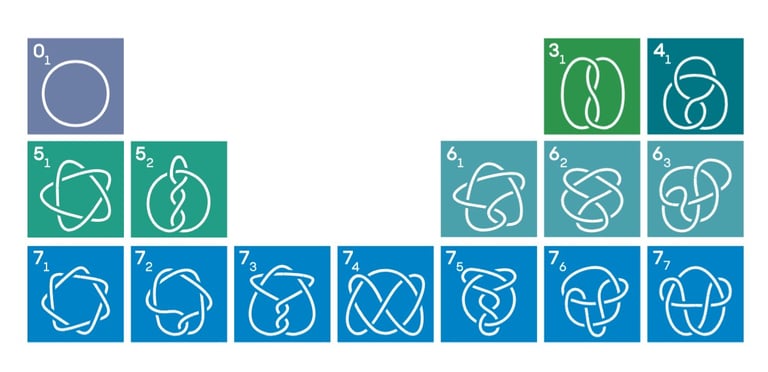
• The Unknot: This is the simplest knot, which is essentially a perfect loop with no crossings. If a knot can be transformed into this by manipulation, it's said to be "unknotted."

• The Trefoil Knot: The trefoil knot has three crossings and is often the first "true" knot that mathematicians have studied.

• Figure-eight Knot: With four crossings, this knot is more complex than the trefoil. It gets its name from its resemblance to the figure-eight shape.

• Higher-order Knots: As the number of crossings increases, knots become more intricate which includes the cinquefoil knot with five crossings

The periodic table of prime knots

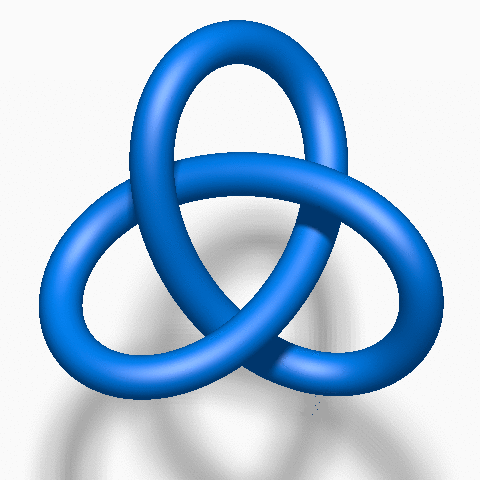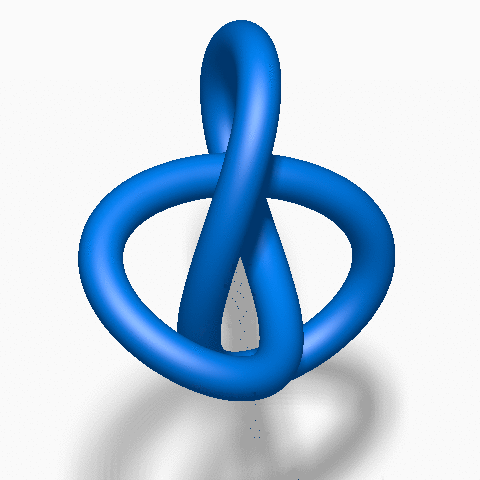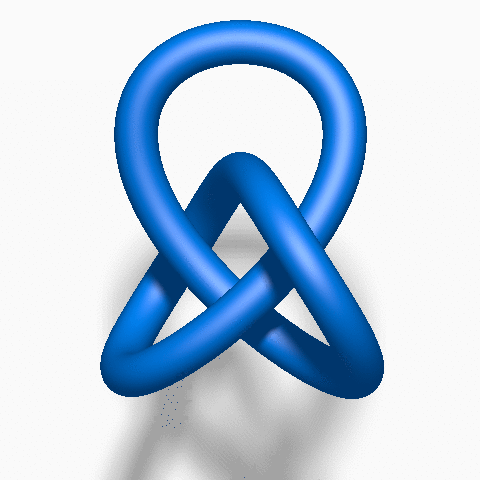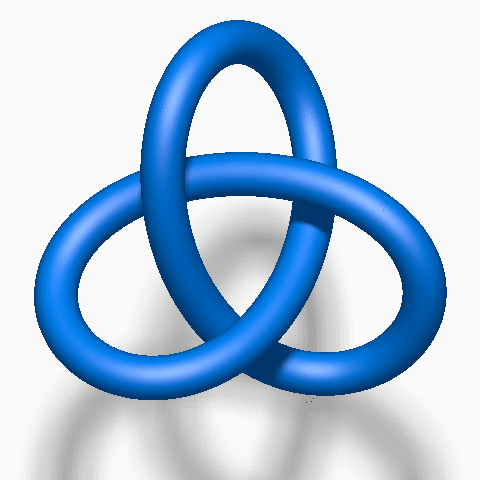
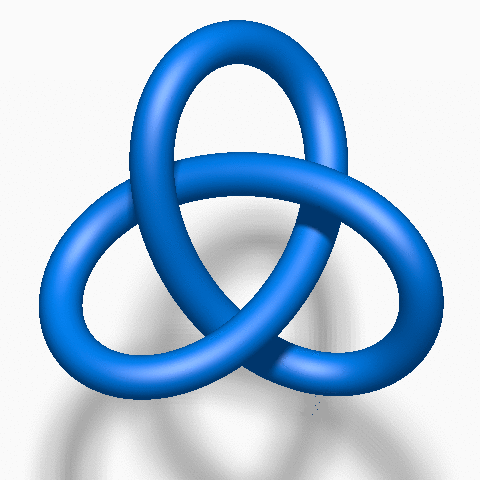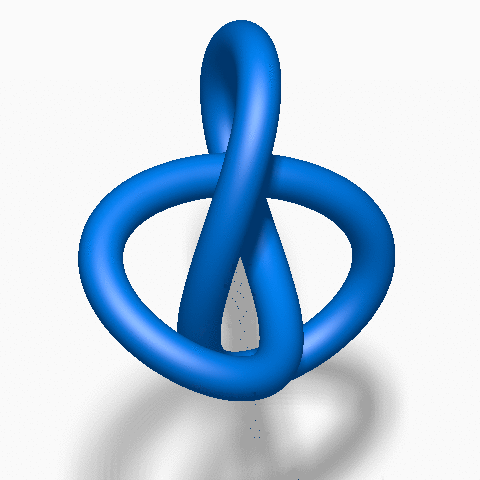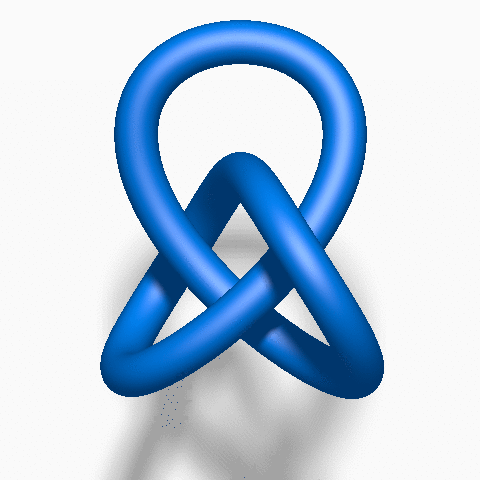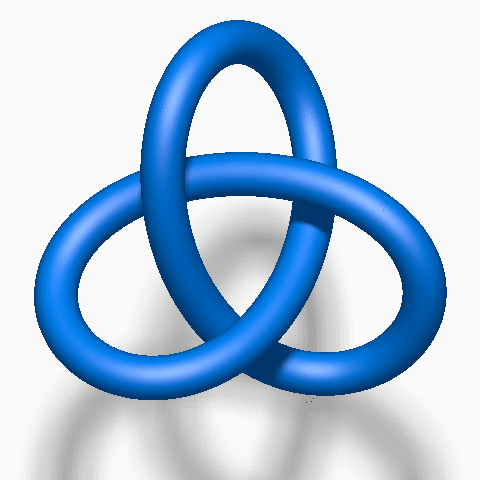
The Unknot

The Trefoil Knot

The Figure-8 Knot